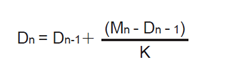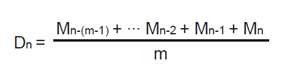功能分享——功率分析仪的平均功能区分方法及详细计算公式！

功率分析仪是一种测量电功率与其他电参数的一种仪器,也可称为电参数分析仪。作为一款测试设备，其功能主要用于电力电子产品电参数的测量。对于功率分析仪中的“隐藏”功能你们都知道那些？今天要分享的是横河功率分析仪中自带的平均功能。它的使用方法一起来学习下吧！

平均功能主要分为两种平均化方法，分别是指数平均与移动平均( 还可成为线性平均)。平均功能主要针对于电源或负载的变动较大或输入信号的频率较低时数值显示不稳定、读取困难的现象有用。两者都具有详细的计算公式说明，可大多数的工程师在实际使用中却不能完全区分这两种平均化方式，甚至是使用使用场景上的区别，对此问题本篇采用计算图表进行简单的说明。

可以经过设置的衰减常数使数据指数平均，可利用下述公式求出平均值。

Dn: 通过第n次指数平均后显示的数值(第1次显示的数值D1等于M1)。

Dn–1: 通过第n-1次指数平均后显示的数值。

Mn: 第n次的测量数据。

K: 衰减常数(从2、4、8、16、32、64中选择)。

可以根据设置的平均个数把数据线性平均，且采用下述公式求出平均值。

Dn: 把第n–(m–1)次到第n次的m个数值数据线性平均后显示的数值

Mn–(m–1): 第n–(m–1)次的测量数据。

Mn–2: 第n–2次的测量数据

Mn–1: 第n–1次的测量数据

Mn: 第n次的测量数据

m: 平均个数(将在8、16、32、64、128、256内选择)。

假如单单大略地看这两个公式，虽然在运算上存在着很大的区别，可是却没有办法让工程师更加直观地理解这类平均化运算对实测测试结果能产生多大的影响，具体平滑处理到什么程度，衰减常数又将怎样选择。下面文章中选取了一段WT5000的DS功能记录的原始波形，利用EXCEL把两种平均方式按不同的衰减常数做出了简单的运算，同时把运算结果与原始波形进行对比。

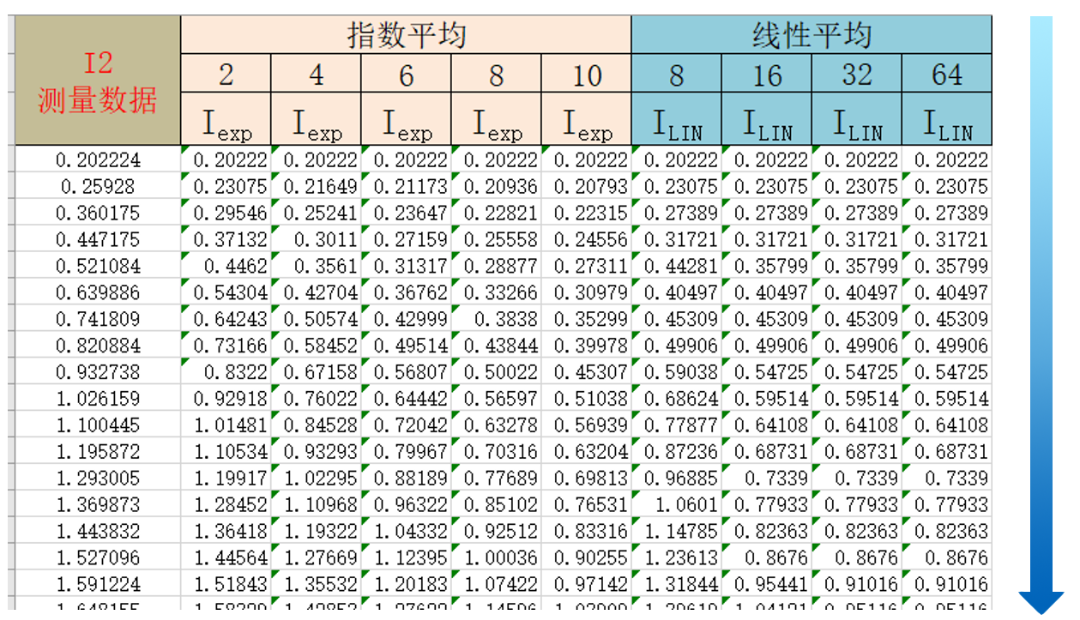
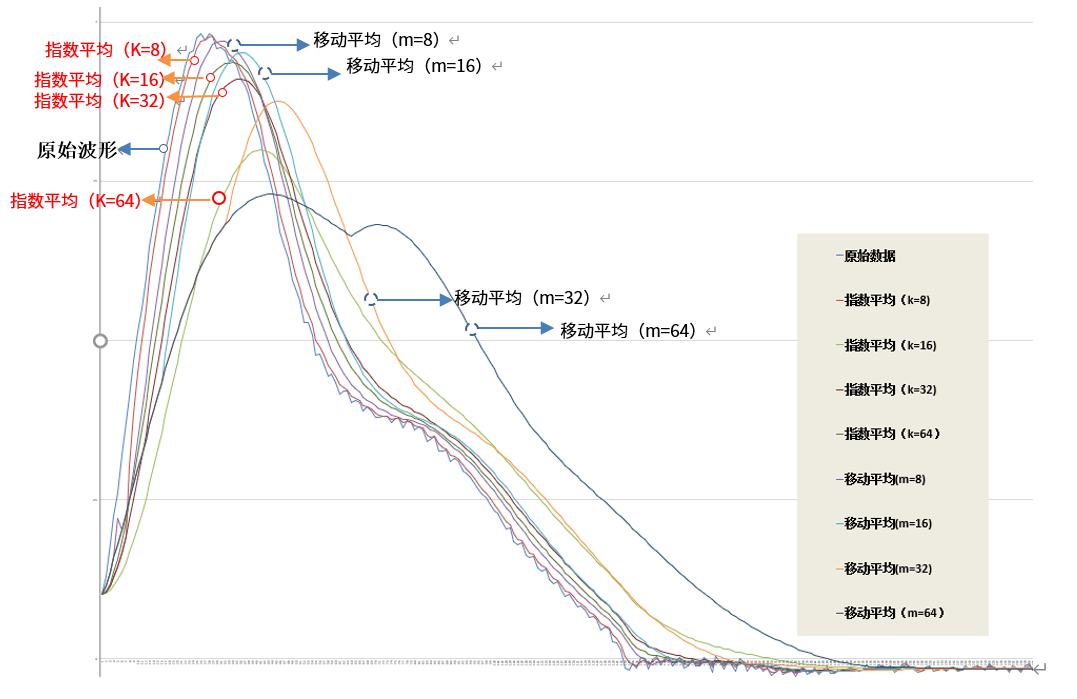
在此因为触及的运算量比较多，这里就选取了指数平均衰减常数2、4、6、8、10，移动平均衰减常数8、16、32、64为例。在上述图中截选了一小部分的运算结果，显然我们面对这个运算结果没有办法对这两种平均化方式有任何直观的认识，因此将全部的运算数据导入二维图表，就可以比较清晰的看出区别了。